- El principio de Arquímedes
- La ecuación fundamental de la estática de fluidos
El aceite que tiene una densidad 0.8 g/cm3 se sitúa en la parte superior y el agua que es más densa 1.0 g/cm3 se sitúa en la parte inferior del recipiente.
La densidad del bloque es un número al azar comprendido entre la densidad del aceite 0.8, y la del agua 1.0. Un cuerpo de esta densidad flota entre los dos líquidos.
Principio de Arquímedes
Conociendo que parte del sólido está sumergido en aceite (fluido 1) o en agua (fluido 2), se determinará la densidad de dicho cuerpo.

Consideremos una esfera de radio R que tiene una densidad ρ<1 y que se mantiene completamente sumergida en agua. Se suelta la esfera y se observa su movimiento oscilatorio
En esta página, vamos a comprobar que su comportamiento difiere del Movimiento Armónico Simple (M.A.S.).
ECUACIÓN DEL MOVIMIENTO.
 Supondremos que el agua y el aire son fluidos ideales, que no ejercen fuerzas de rozamiento sobre la esfera en movimiento.
Supondremos que el agua y el aire son fluidos ideales, que no ejercen fuerzas de rozamiento sobre la esfera en movimiento.
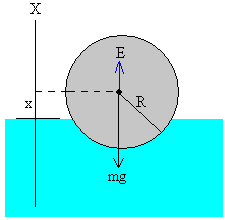
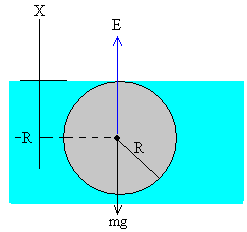
Para describir el movimiento, situamos el origen del eje X en la superficie del agua y llamamos x a la posición del centro de la esfera.
- Cuando x=-R, la esfera se encuentra completamente sumergida
- Cuando x=+R la esfera se encuentra justamente fuera del agua
- El peso mg
- El empuje E
Para una esfera de densidad ρ relativa al agua (cuya densidad es la unidad) la masa es
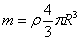
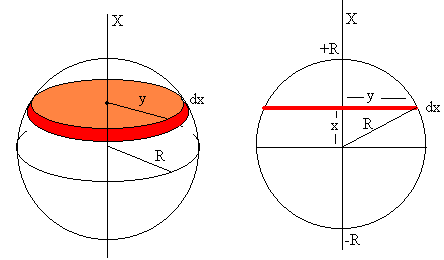
El empuje es el peso en agua del volumen de la parte sumergida. Calculamos el volumen de la parte de la esfera sumergida en agua. Este volumen V es la suma (integral) de los elementos diferenciales de volumen de radio y y de altura dx, uno de los cuales se muestra en la figura.
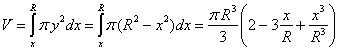
|
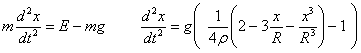
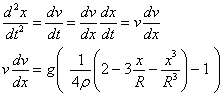
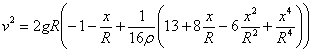
No hay comentarios:
Publicar un comentario